Research article

Las jerarquías conceptuales en UML: comparando la norma ISO 2788 con el metamodelo de UML

Conceptual hierarchies in UML: comparing ISO 2788 standard with the UML metamodel

Resumen

En este artículo llevamos a cabo una comparación entre dos enfoques del modelado de la estructura jerárquica del mundo real: por una parte, las relaciones genérico y todo-parte en un tesauro de descriptores; por otra parte, las relaciones de generalización y agregación en UML. El intento de acortar la distancia entre ambos enfoques conduce a un nuevo metamodelo de relaciones que puede reflejar mejor los hábitos mentales de los modeladores cuando tratan con árboles jerárquicos.

Abstract

In this article we perform a comparison between two approaches to the modeling of the hierarchical structure of the real world: on the one hand, generic and whole-part relationships in a descriptors thesaurus; on the other hand, generalization and aggregation relationships in UML. Trying to shorten the distance between them leads to a new metamodel of relationships that can reflect better the mental habits of modelers when dealing with hierarchical trees.

Palabras Clave:

modelado de la estructura jerárquica, lenguaje Unificado de Modelado, árboles jerárquicos

Keyword:

hierarchical trees, ,

Introducción

Research at the Information Engineering Group of the Department of Computer Science, Carlos III University of Madrid, is centered around software reuse. We are concerned with high-level reuse, which implies not only codereuse, but also (and mainly) analysis and design models reuse. We have been working for years with descriptors thesauri in order to represent specific domains, trying to extract the internal structure of a piece of software from the structure of the real world it models or implements. When we incorporated the Unified Modeling Language in our methodology, it was only a question of time that a comparison between both approaches to model the real world would arise. One of the aspects of this comparison is the modeling of hierachies.

The systematic organization of a conceptual hierarchy representing the structure of the world has been addressed in many different ways along history. Fritz Lehmann lists as much as 178 different concept catalogues, taxonomies and hierarchies (including high level "ontologies") for possible use in knowledge representation, artificial intelligence, simulation, and database integration, from Aristotle's categories to Sowa's dimensional ontology [Leh]. Among these concept systems, those based on thesauri of controlled vocabulary have become widely used in fields such as information retrieval and may be chosen as good representatives of conceptual hierarchies.

The hierarchical relationship most distinguishes a systematic thesaurus from an unstructured list of terms, for example a glossary or dictionary. It is based on degrees or levels of superordination and subordination, where the superordinate term represents a class or whole, and subordinate term refers to its members or parts [MTh 8.3.1]. There are three logically different kinds of hierarchies in a thesaurus:

• The generic relationship identifies the link between a class or category and its members or species [MTh 8.3.4.1]. Examples:
  • cars
    • diesel cars
    • electric cars
  • animals
    • birds
      • parrots
• The whole-part relationship applies to four main classes of terms: systems and organs of the body, geographical locations, disciplines or fields of discourse, and hierarchical social structures [MTh 8.3.5.1]. Examples:
  • circulatory system
    • cardio-vascular system
      • arteries
      • veins
  • Canada
    • Ontario
      • Ottawa
      • Toronto
    • Alberta
  • Science
    • Physics
    • Biology
      • Botany
      • Zoology
  • Armies
    • Corps
      • Divisions
        • Battalions
        • Regiments
• The instance relationship identifies the link between a general category of things or events, expressed by a common noun, and an individual instance of that category, represented by a proper name [MTh 8.3.6.1]. Example:
  • Mountain
    • regions
      • Alps
      • Himalayas

This third kind of relationship is somewhat different from the other, since it does not relate two concepts, but a concept and an instance of that concept. Therefore, only the first two kinds of relationships, generic-specific and whole-part, are significative in the construction of a conceptual system with several hierarchical levels.

Generalization and aggregation in UML: similarities and differences

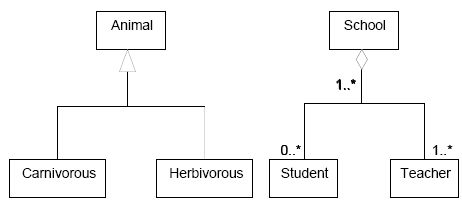
Generic-specific and whole-part relationships between concepts correspond to generalization and aggregation between classes in the Unified Modeling Language (UML), which was designed by Grady Booch, James Rumbaugh and Ivar Jacobson as a graphical language for specifying, constructing, visualizing and documenting software-intensive systems from an object-oriented perspective. In object orientation, by contrast with a thesarurus environment, a class is not only an abstract description of a concept, but also a frame used to build a set of concrete objects (or instances) with common structural and behavioral features, via a process referred to as instantiation. In UML, a concept (that is, a class) is rendered as a rectangle, and a relationship as a solid line between two classes, possibly with a special terminator in one of its ends, and other adornments. Generalization and aggregation relationships in UML are vaguely similar in that both admit a tree-style of drawing:

Two kinds of hierarchical trees: generalization and aggregation

In spite of these similarities, hierarchical character and drawing style, there exist deep differences in the semantics of both kinds of relationships in UML:

It can be observed that this differences derive mainly from the fact that an association (and therefore an aggregation) is an abstraction of the links that may exist between object instances of the related classes, while a generalization is not. An object may be a part of a composite object, but it can never be the specialization of a more general object, because an object is always concrete; specialization has sense only at the conceptual level, not at the instance level. This implies also that adornments like multiplicity, which express abstract properties of the concrete links, may be placed on aggregation ends, but have no sense by generalizations.

UML metamodel of relationships

In order to furnish a formal basis for understanding the Unified Modeling Language, the Object Management Group (the organization involved in its standardization) provides a formal definition of the language using UML class diagrams, that is, they use a subset of the language to define itself: this is called a metamodel.

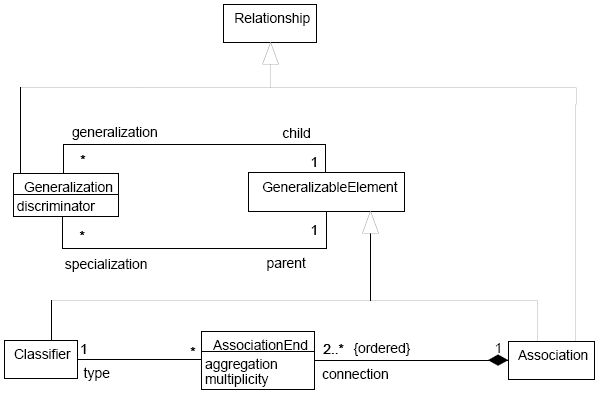Simplified metamodel of relationships (UML 2.5.2, Figure 2-6)

UML metamodel for generalizations

According to the metamodel represented in the previous figure and some statements drawn from the UML Semantics [UML part 2] and the UML Notation Guide [UML part 3], generalizations have the following properties:

• Generalizations are binary relationships: "Generalization is the taxonomic relationship between a more general element (the parent) and a more specific element (the child)" [UML 3.49.1]. This is represented in the metamodel as a metaclass Generalization which has a GeneralizableElement playing the role of the parent, and another GeneralizableElement playing the role of the child [UML 2.5.2].
• Generalizations may have partitions: "A generalization path may have a text label called a discriminator that is the name of a partition of the children of the parent. The child is declared to be in the given partition" [UML 3.49.2]. This is represented in the metamodel with the metaattribute Generalization.discriminator [UML 2.5.2].
• Different generalizations with the same parent may have the same discriminator, meaning that they belong to the same partition: "The discriminator must be unique among the attributes and association roles of the given parent. Multiple occurrences of the same discriminator name are permitted and indicate that the children belong to the same partition" [UML 3.49.2].

Classification with discriminators

There are two styles of drawing classifications in UML, separated target style and shared target style: "A group of generalization paths for a given parent may be shown as a tree with a shared segment (including the triangle) to the parent, branching into multiple paths to each child" [UML 3.49.3].

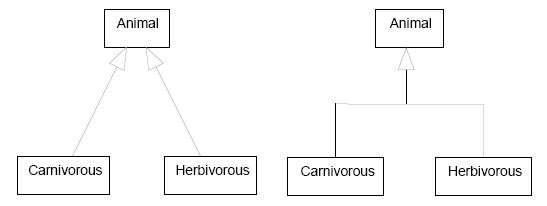Two styles of drawing the same classification

Boths styles are perfectly synonymous, and modelers must choose one or the other for aesthetic concerns only, without semantic intention: "A generalization tree with one arrowhead and many tails maps into a set of Generalizations, one between each element corresponding to a symbol on a tail and the single GeneralizableElement corresponding to the symbol on the head. That is, a tree is semantically indistinguishable from a set of distinct arrows, it is purely a notational convenience" [UML 3.49.5].

UML metamodel for aggregations

Conversely, the metamodel tells us the following properties of aggregations:

• Aggregations are a special kind of binary associations: "An association may represent an aggregation (i.e., a whole/part relationship). In this case, the association-end attached to the whole element is designated, and the other association-end of the association represents the parts of the aggregation. Only binary associations may be aggregations" [UML 2.5.4]. "A hollow diamond is attached to the end of the path to indicate aggregation" [UML 3.42.2]. This is represented in the metamodel with the metaattribute AssociationEnd.aggregation [UML 2.5.2].
• Aggregations are always binary relationships between the whole and the part, that is, n-ary associations cannot have an aggregation end: "An n-ary association may not contain the aggregation marker on any role" [UML 3.46.1].

There are also two styles of drawing aggregations in UML, separated target style and shared target style, but both styles are perfectly synonymous: "If there are two or more aggregations to the same aggregate, they may be drawn as a tree by merging the aggregation end into a single segment. This requires that all of the adornments on the aggregation ends be consistent. This is purely a presentation option, there are no additional semantics to it" [UML 3.42.3].

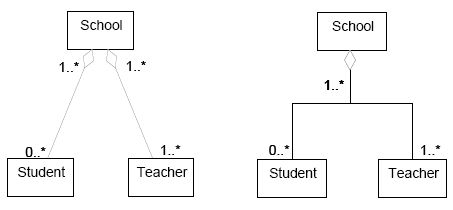Two styles of drawing the same aggregation

That is, like generalization trees, an aggregation tree with one arrowhead and many tails maps into a set of Associations, one between each Classifier corresponding to a symbol on a tail and the single Classifier corresponding to the symbol on the head, with the aggregation property designated on each AssociationEnd on the side of the head. That is, a tree is semantically indistinguishable from a set of distinct arrows, it is purely a notational convenience.

Towards a new metamodel of relationships

A new metamodel for generalizations

As we have seen, according to UML there are two styles of drawing both generalizations and aggregations, as a tree or as a set of distinct arrows, both of them being perfectly synonymous, that is, semantically indistinguishable. But is this reallistic?

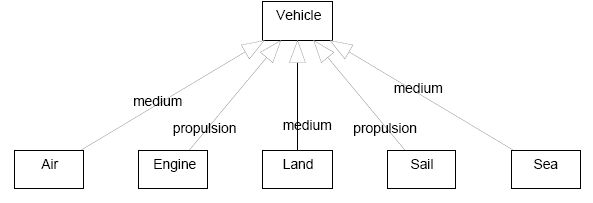
Modelers usually employ the tree-style of drawing generalizations to express different “dimensions of classification”; that is, the subclasses in the same branch of the tree specialize the superclass according to the same criterion or dimension. The use of trees renders a classification clearer when two or more dimensions are present in it.

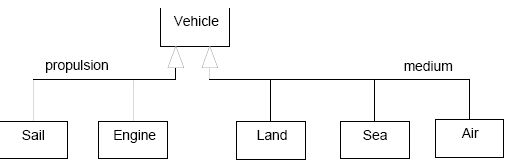Classification according to independent dimensions using trees. Compare with the previous diagram used to classify vehicles, in which the lack of ordering in discriminators makes it difficult even to notice that there are two dimensions

But, we can say, whenever there is a will to express some property of the model, to transmit some information about it, we must recognize a semantic intention, not only an aesthetic one. By contrast, we can say the difference between rectilinear and diagonal lines representing relationships is purely aesthetical.

On the other side, being the metaattribute Generalization.discriminator not a sheer adornment of the generalization, but a real property of the model, it must be acknowledged that this semantic intention is sufficiently recognized by the UML: there is nothing expressed in the tree-style that be not represented with the discriminator metaattribute, but clarity of graphical expression (something useful for human modelers, but not significant for, say, a CASE Tool).

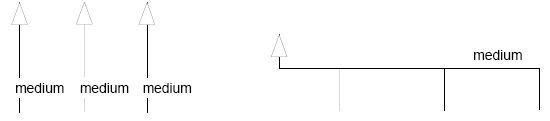Three modeling elements or one modeling element? A dimension of specialization may be modeled as group of named binary classifications with a common discriminator attribute, or else as a single named classification tree with one parent and several children

Sufficiently recognized, we say, but probably the solution UML gives in the metamodel to the representation of these various dimensions of classification might be improved by a good deal: it doesn't seem a good objectoriented practice to state that "two generalizations are in the same partition if they have a common discriminator", this being specified as a literal attribute: "Discriminator: Designates the partition to which the Generalization link belongs. All of the Generalization links that share a given parent GeneralizableElement are divided into groups by their discriminator names. Each group of links sharing a discriminator name represents an orthogonal dimension of specialization of the parent GeneralizableElement" [UML 2.5.2]. Therefore, having each dimension of specialization its own identity, and being the "identity" one of the three main characteristics of objects, along with its "state" and "behavior" [BRJ 11], the standard practice would be to consider the classification tree as a metaobject on its own. This may be achieved with a very slight change in the metamodel of generalizations, namely the multiplicity on the child side:

Proposed metamodel for generalization trees

In addition, the metaattribute Generalization.discriminator is no longer needed, since the other metaattribute ModelElement.name, inherited by Generalization, serves perfectly for the purpose of naming both the generalization and the dimension of specialization, being in this metamodel the same thing.

A new metamodel for aggregations

Although aggregations may also be drawn using the tree-style, there seems to be nothing in UML analogous to the "dimensions of classification", at least the metamodel does not recognize anything like "dimensions of partition" for aggregations. For this to have some sense for modelers, we ought to find cases in the real world in which a whole is divided into parts according to different criteria. Usually an aggregation association is instantiated by a number of aggregation links; that is, each aggregation association relates the whole with a kind of parts, thus being each aggregation association somehow a kind of partition; since each aggregation association may be considered itself a criterion of division of the whole into its parts, we must further determine if there is something that a group of aggregations may have in common and that another group has not, thus rendering sensible the use of separated aggregation trees.

From an abstract point of view, we can divide a whole into parts according to spatial, temporal, or logical dimensions (and possibly other abstract categories of division, like the twelve kantian categories), that is, dimensions whose elements are heterogeneous and should not be mixed. From a more concrete point of view, as it was stated above, for an aggregation to be drawn as a tree, it is required that all of the adornments on the individual aggregation ends be consistent (mainly AggregationKind and Multiplicity). These two points of view, not necessarily disjoint, give us some clues about what these "dimensions of partition" may signify in a real problem.

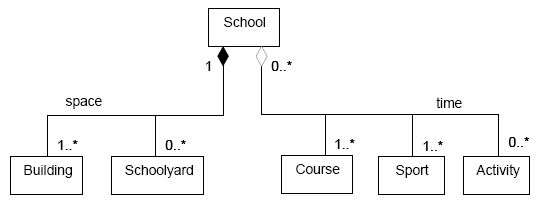Partition according to independent criteria using trees

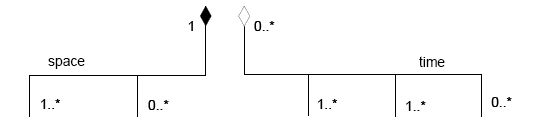Five modeling elements or two modeling elements? A dimension of partition may be modeled as a group of binary aggregations with common adornments and role name on the aggregate side, or else as a single named aggregation tree with one whole and several kinds of parts

The status of the "dimensions of partition" in aggregations (wether they have or not their own "identity") may be said to be weaker than that of "dimensions of classification" for generalizations, and consequently the conceptual need to consider aggregation trees as metaobjects and have a representation in the UML metamodel is not so clear. Nevertheless, we can specify how could the corresponding metamodel be:

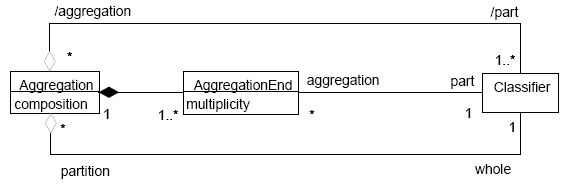Proposed metamodel for aggregation trees. Derived roles are shown for comparison with the metamodel for generalization trees. Note that AggregationEnd is not semantically equivalent to an association-class, since a given Classifier could play several roles as "part" in the same Aggregation (see Martin Fowler, UML Distilled, pp. 93-95)

The changes performed on the metamodel of aggregations are not so slight as those on the metamodel of generalizations. On the contrary, it is necessary to introduce two new metaclasses, Aggregation and AggregationEnd, since aggregations may no longer be considered special cases of associations, due to their inherently asymmetric character. This can have some advantages too, since the actual metamodel needs a number of constraints added to the basic class diagram to represent the semantics of aggregations ("at most one AssociationEnd may be an aggregation", and "no AssociationEnd may be an aggregation on an n-ary Association", [UML 2.5.3]), which are no longer needed in the proposed metamodel. The name of the dimension of partition, that is, the role name of the whole, is represented by the metaattribute ModelElement.name, inherited by Aggregation; each part can have also a role name on its own (ModelElement.name inherited by AggregationEnd). The kind of aggregation (simple weaker aggregation or stronger composition) is no longer represented in each aggregation end, but only once by boolean metaattribute Aggregation.composition.

A new unified metamodel of relationships

When both new proposed metamodels for hierachical conceptual trees are merged into the UML metamodel for relationships, we can observe that some sort of n-arity in generalizations and aggregations has been added to the metamodel, since a “dimension of classification” (or a "dimension of partition") is by nature a n-ary asymmetric relationship, with one head, the superclass (or the whole), and multiple legs, the subclasses (or the kinds of parts), thus breaking the common principle that both generalizations and aggregations are binary relationships.

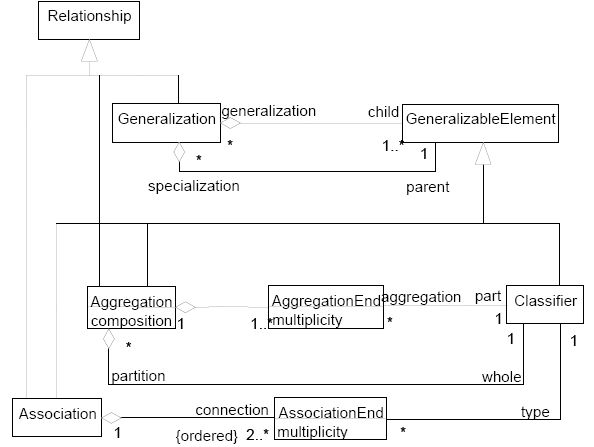Simplified proposed metamodel for classification and aggregation trees

Conclusions

In object orientation, by contrast with a thesarurus environment, a class is not only an abstract description of a concept, but also a frame used to build a set of concrete objects (or instances) with common structural and behavioral features, via a process referred to as instantiation.

Generic-specific and whole-part relationships between concepts in a thesaurus correspond to generalization and aggregation between classes in the Unified Modeling Language, which are vaguely similar in that both admit a tree-style of drawing. But in spite of these similarities, hierarchical character and drawing style, there exist deep differences in the semantics of both kinds of relationships in UML, derived mainly from the fact that an association (and therefore an aggregation) is an abstraction of the links that may exist between object instances of the related classes, while a generalization is not.

The solution UML gives in the metamodel to the representation of the various dimensions of classification (the use of literal discriminators) might be improved by considering the classification tree as a metaobject on its own. This may be achieved with a very slight change in the metamodel of generalizations, namely the multiplicity on the child side.

The status of the "dimensions of partition" in aggregations may be said to be weaker than that of "dimensions of classification" for generalizations, and consequently the conceptual need to consider aggregation trees as metaobjects and have a representation in the UML metamodel is not so clear. The changes performed on the metamodel of aggregations would not be so slight as those on the metamodel of generalizations, and aggregations would cease to be considered special cases of associations.

Notas

Este trabajo fue presentado en el Workshop on Defining Precise Semantics for UML, incluido en The 14th European Conference on Object-Oriented Programming-ECOOP'2000, 12-16 Junio 2000, Sophia Antipolis-Cannes, France. El Comité Editorial lo ha seleccionado para su publicación dado su interés para la Revista Técnica Administrativa

Bibliografía - Bibliography

Booch, G., Rumbaugh, J., Jacobson, I. The Unified Modeling Language User Guide. Addison-Wesley, 1999.

ISO International Standard 2788. Documentation - Guidelines for the establishment and development of monolingual thesauri. Second Edition, 1986.

Object Management Group, Unified Modeling Language Specification (draft), Version 1.3 alpha R5, March 1999.

Lehmann, F., Concept-Systems Catalogue, Version 5, July 1996.

Google Scholar Index

Article

Las jerarquías conceptuales en UML: comparando la norma ISO 2788 con el metamodelo de UML

Publisher:

Ciencia y Técnica Administrativa - CyTA