Research article
Una Aplicación del Método de Monte Carlo en el Análisis de Riesgo de Proyectos: Su automatización a través de una planilla de cálculo
An application of the Monte Carlo Method in the Risk Analysis of Proyects: Its authomatization through an electronic spreadsheet
Perissé, Marcelo Claudio ⓘ
Doctor en Ciencias Económicas
Magister en Informática.
Secretaría de Ciencia y Tecnología, Universidad Nacional de La Matanza
San Justo, Buenos Aires. Argentina
Resumen
En este trabajo se presenta, a través de un caso práctico, la utilización de la planilla electrónica en el análisis de rentabilidad de inversiones bajo riesgo. Específicamente se describe como operar el producto Microsoft Excel, para llevar adelante la construcción del método de Monte Carlo aplicado la evaluación de proyectos de inversión.
Abstract
This article presents, through a practical case, the utilization of the electronic spreadsheet in the return analysis of investments under risk. Specifically , it is described how to operate the Microsoft Excel product in order to develope the construction of the Monte Carlo method applied to the evaluation of investment proyects.
Palabras Clave:
RIESGO, CONSOLIDACION DE LA DEUDA, ADMINISTRACION ⓘ
Keyword:
Método de Monte Carlo, Risk analysis, simulation ⓘ - ⓘ - ⓘ - ⓘ
1.- Introducción
El método de Monte Carlo es una herramienta de investigación y planeamiento; básicamente es una técnica de muestreo artificial, empleada para operar numéricamente sistemas complejos que tengan componentes aleatorios.
Gracias a la constante evolución de las microcomputadoras, en lo que se refiere a su capacidad de procesamiento de la información, el método de Monte Carlo es cada ves más frecuentemente utilizado.
Esta metodología provee como resultado, incorporada a los modelos financieros, aproximaciones para las distribuciones de probabilidades de los parámetros que están siendo estudiados.
Para ello son realizadas diversas simulaciones donde, en cada una de ellas, son generados valores aleatorios para el conjunto de variables de entrada y parámetros del modelo que están sujetos a incertidumbre. Tales valores aleatorios generados siguen distribuciones de probabilidades específicas que deben ser identificadas o estimadas previamente.
Vale destacar que el concepto de simulación, adoptado en este trabajo, es el descripto en los estudios de Robert E. Shannon [1975] donde la Simulación es el proceso de diseñar y desarrollar un modelo computarizado de un sistema o proceso y conducir experimentos con este modelo, a fin de entender el comportamiento del sistema o evaluar varias estrategias con las cuales se puede operar el sistema. El conjunto de resultados, producidos a lo largo de todas las simulaciones, podrán ser analizados estadísticamente y proveer resultados en términos de probabilidad. Esas informaciones serán útiles en la evaluación de la dispersión total de las apreciaciones del modelo, causado por el efecto combinado de las incertidumbres de los datos de entrada y en al evaluación de las probabilidades de ser violados los padrones de las proyecciones financieras.
En lo que se refiere al uso de la computadora, podemos asegurar que los procedimiento a desarrollar para obtener una visión clara de la variabilidad y el rédito de los proyectos bajo análisis, requerirá de técnicas simples; como por ejemplo, y lo vamos a mostrar en este trabajo, la planilla de cálculo puede emplearse para obtener valiosa información sobre la sensibilidad del posible rendimiento frente a las variaciones de factores determinados, y sobre la probabilidad de obtener diversos niveles de rendimiento.
Esta información será fundamental como respaldo de decisiones gerenciales; no pueden quedar dudas que el conocimiento de la probabilidad de ocurrencia de toda la gama de posibles rendimientos, brinda una cierta seguridad de que la información disponible ha sido empleada con la máxima eficacia.
El ejercicio de razonar en base a la incertidumbre contribuye a mejorar la habilidad de elegir las inversiones, porque comprender la incertidumbre y el riesgo equivale a comprender el secreto de los negocios, y es la llave para abrir la puerta a la buenas oportunidades.
2.- Automatización del Modelo de Monte Carlo
De forma simplificada, se puede aplicar el Modelo de Monte Carlo en el Excel de la siguiente forma:
1. Estimar la escala de valores que podría alcanzar cada factor, y la probabilidad de ocurrencia asociada a cada valor.
2. Elegir, aleatoriamente, uno de los valores de cada factor, y dependiendo de la combinación seleccionada, computar la tasa de rendimiento resultante.
3. Repetir el mismo proceso una y otra ves, la cantidad de veces que sea necesaria, que permita definir y evaluar la probabilidad de ocurrencia de cada posible tasa de rendimiento. Como existen millones de posibles combinaciones de factores, necesitamos efectuar un número de pruebas suficientemente grande para que pueda apreciarse la posibilidad de ocurrencia de las varias tasas de rendimiento. El resultado al que se llegará será una lista de distintas tasas de rendimiento que podrían lograrse, que puede variar desde una pérdida (si los factores son adversos) hasta la ganancia máxima que sea posible lograr conforme con los pronósticos que se hayan efectuado.
4. Se calcula la tasa media esperada, que es el promedio ponderado de todas las tasas resultantes de las sucesivas pruebas realizadas, siendo la base de ponderación la probabilidad de ocurrencia de cada una.
5. También se determina la variabilidad de los valores respecto del promedio, lo que es importante porque a igualdad de otros factores, la empresa presumiblemente preferirá los proyectos de menor variabilidad.
Dependiendo de la política de decisión, el proceso lo podremos aplicar a la tasa interna de retorno o al valor actual neto. Los ejercicios aquí presentados trabajan en base al valor actual neto.
3.- Ejercicios
Se presentan dos problemas de selección de inversiones mediante los criterios del Valor Actual Neto (VAN); ambos problemas contienen la determinación de una estimación de los flujos de caja pesimista, más probable y optimista que genera la inversión en un período de tiempo.
El modelo del Valor Actual Neto (VAN) se aplica para valorar todos los rendimientos del proyectos de inversión al momento de su inicio, y obedece a la fórmula:
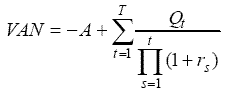
donde A es es desembolso inicial del proyecto; T su duración; Qt, t=1,..., T, el flujo de caja producido en el período t; y rs, s=1,...,t, la tasa de descuento aplicable en dicho período.
Para distribuciones discretas
Bastaría colocar la distribución discreta basada en la función de probabilidad acumulada (entre 0% y 100%), generar un número aleatorio y a través de una función de búsqueda y referencia, como la función buscar, identificar el valor correspondiente.
Aplicando conjuntamente las funciones "buscar" y "aleatorio", se puede asegurar la aleatoriedad de los posibles Valores Actuales Netos (VAN) obtenidos, y que luego de "n" simulaciones ("n" no debería ser menor a 1.000) , permitiría calcular el promedio y el desvío de la distribución, que para nuestro caso de estudio financiero estaría asociado al riesgo de la inversión.
Veamos un ejemplo
|
||||||||||||||||||||||||||||||||||||
|
(1)=BUSCAR(ALEATORIO();C3:C5;A3:A5) |
||||||||||||||||||||||||||||||||||||
| Tabla 1. Flujos de caja pesimista, más probable y optimista |
Si hacemos mil simulaciones encontraremos que el promedio y el riesgo tienden a estabilizarse próximos a los valores poblacionales anteriormente calculados. Recuerde que para activar la fórmula aleatorio debe presionar la tecla F9.
|
||||||||||||||||||||
|
En la celda A11 corresponde =BUSCAR(ALEATORIO();$C$3:$C$5;$A$3:$A$5) En la celda B11 corresponde =PROMEDIO($A$11:A11) En la celda C11 corresponde =DESVEST($A$11:A11) |
||||||||||||||||||||
| Tabla 2. Función buscar combinada con función aleatorio e identificación del VAN correspondiente |
Ploteando el gráfico de los números de simulaciones con los valores del promedio y el desvío, puede percibirse que próximo a las 200 simulaciones, los valores se tienden a estabilizar.
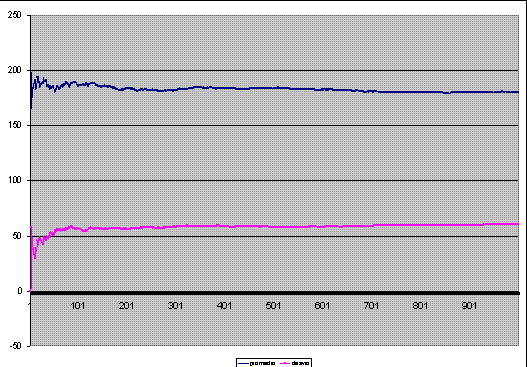
Figura 1. Representación del promedio y del desvío correspondiente a la Tabla 1.
Distribuciones Continuas:
En nuestro modelo de simulación estocástico, existen varias variables aleatorias intercatuando. Y estas variables, siguen distribuciones de probabilidad teóricas o empíricas distintas a la distribución uniforme. Por esta razón, para simular este tipo de variables, es necesario contar con un generador de números uniformes y una función que a través de un método específico, transforme estos números en valores de distribución normal.
Existen varios procedimientos para lograr este objetivo, en este trabajo se adoptó el siguiente procedimiento especial para generar números al azar que sigan la distribución de probabilidad.
Para cada tipo de distribución continua, se puede montar una función
estocástica; en nuestro caso, una distribución normal puede ser expresado
por:
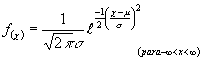
para expresar la distribución acumulada de la distribución normal en forma explícita, utilizamos el teorema del límite central, el cual establece que la suma de n variables aleatorias independientes se aproxima a una distribución normal a medida que n se aproxima a infinito.
Que expresado en forma de teorema sería:
Si x1,x2,.......xn es una secuencia de n variables aleatorias independientes con E(x)=µi y var (x)= ð2i (ambas finitas) y Y= a1x1+a2x2+.....+anxn, entonces bajo ciertas condiciones generales:
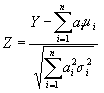
Tiene una distribución normal estándar a medida que n se aproxima a infinito. Si las variables que se están sumando son uniformes en el intervalo (0;1) entonces:
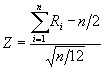
donde R es un número aleatorio.
Tiene una distribución normal estándar. Puesto que la normal estándar de una variable aleatoria x distribuida normalmente se obtiene como:
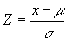
entonces, la simulación de la variable aleatoria x se haría de acuerdo a la siguiente expresión:
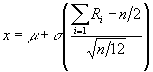
Finalmente, utilizando un valor de n=12, la confiabilidad de los
valores simulados es bastante aceptable. Y utilizando un valor de n=12, la
última expresión se simplifica a:
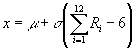
Para hacer esta operación en el Excel, se debe usar la función =aleatorio().
=((((ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+
ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO())-6)*Desvío
+ Promedio))
Una alternativa a este modelo es aplicar la función, de la planilla electrónica Excel, DISTR.NORM.INV, que devuelve el inverso de la distribución acumulativa normal para la media y desviación estándar especificadas.
A continuación se presenta un ejemplo de la utilización del método de Monte Carlo en la planilla de Microsoft Excel. Estos son los datos del Ejercicio:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabla 3. Datos del Proyecto de Inversión | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Luego se comienza a construir el Modelo.
Para cada tipo de gaseosa se calcula:
El Acumulando de las probabilidades.
El promedio y el riesgo.
Se aplican las funciones: aleatrorio y buscar
Se aplica la función estocástica para determinar la cantidad.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| (1)
=SUMAPRODUCTO(B13:B15;$A$13:$A$15) (2) =SUMAPRODUCTO(($A$13:$A$15-SUMAPRODUCTO(B13:B15;$A$13:$A$15))^2;B13:B15)^(1/2) (3) =BUSCAR(ALEATORIO();B23:B25;$A$13:$A$15) (4) =ENTERO(((((ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ALEATORIO()+ ALEATORIO()+ALEATORIO()+ALEATORIO())-6)*B19+B18))) o bien en (4) puede utilizar =DISTR.NORM.INV(ALEATORIO();B18;B19) Se repite el proceso para cada producto restante |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabla 4. Cálculo de las probabilidades acumuladas para cada producto |
Luego y en función de estos valores se procede al cálculo del Valor Actual Neto, utilizando la función predeterminada del Excel VNA; recuerde que la inversión inicial correspondiente al momento 0, va leteando a esta función.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Las ecuaciones para el primer período se repiten para los 19 períodos restantes | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabla 5. Representación del Flujo de Fondos y cálculo del Valor Actual Neto del proyecto | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Una vez que se tiene la estructura para el cálculo del Valor Actual Neto, se puede realizar una macro que valla acumulando los registros de cada valor puntual que correspondan al Valor Actual Neto, a medida que se activa la función aleatoria para cada simulación. Además se puede ir calculando los valores correspondientes del promedio y del desvío, a fin de poder estudiar el comportamiento del modelo.
|
|||||||||||||||||||||||||||||||||||
| Tabla 6. Simulación de Monte Carlo |
La macro para realizar este proceso puede tener las siguientes instrucciones:
Esta macro requiere que:
- El nombre de la hoja donde se ejecute el proceso se denomine: "Jugadas"
- El nombre de la hoja donde se encuentra el resultado del VAN (ver Tabla 5.) se denomine: "Hoja1"
| Sub montecarlo() ' imprime un contador de 1 a 1000 ' imprime una lista de 1000 valores resultantes de Monte Carlo For Fila_Juego = 1 To 1000 'comentario: Fila_Juego representa la Fila 1 Juego = Juego + 1 ' Juego representa una constante que acumula ' el valor anterior y suma uno ' y se posiciona en la celda (Cells(Fila_Juego + 1, 1)) ' indicada por "Fila_Juego+1" que indica la fila y ' la columna 1 o "A" Worksheets("jugadas").Cells(Fila_Juego + 1, 1) = Juego Next Fila_Juego For Fila_van = 1 To 1000 van = Worksheets("Hoja1").Range("B50") ' la variable van asume el valor de la celda "B50" de la Hoja1 Worksheets("jugadas").Cells(Fila_van + 1, 2) = van ' la variable se registra en la segunda columna Next Fila_van For Fila_Promedio = 1 To 1000 Promedio = "=AVERAGE(R2C2:RC[-1])" ' calcula el promedio del van fila 2 columna 2(R2C2) y ' lo acumula RC[-1], es lo mismo que $B$2:B2 Worksheets("jugadas").Cells(Fila_Promedio + 1, 3) = Promedio Next Fila_Promedio For Fila_Desvio = 1 To 1000 Desvio = "=STDEV(R2C2:RC[-2])" Worksheets("jugadas").Cells(Fila_Desvio + 1, 4) = Desvio Next Fila_Desvio End Sub
|
| TAbla 7. Procedimiento en Microsoft Visual Basic 6.3 |
Se puede construir el Histograma correspondiente a los valores del Valor
Actual Neto, para ello se recurre a la opción Histograma localizada en el
Análisis del datos, que se encuentra en Herramientas del asistente;
utilizando la función de Análisis de datos.
|
|
| Figura 2. Uso de la Herramienta Análisis de datos, Histograma |
Al construir el Histograma se cuenta con la opción de realizar el gráfico
automáticamente y además adicionar el porcentaje acumulado.
Con los datos de la tabla que se encuentran el promedio y el riesgo del Valor Actual Neto, se construye el gráfico del Promedio y del desvío muestral por número de simulaciones.
También de forma muy simple se puede construir, en la misma hoja donde se realizó la simulación de Monte Carlo, un sistema una estructura de análisis que contenga el promedio, el desvío, un intervalo de confianza y realizar una distribución de frecuencia; al aplicar la función frecuencia del Excel hay que recordar que ésta es del tipo matricial por lo que requiere que primero se realice la primera función (en el ejemplo está en la celdaI2) luego se marca el rango de celdas al que se va a copiar, posicionaos en la celda I2 se edita con la tecla F2 y por último se ejecuta simultaneamente las teclas ctrl+Shift+Enter.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
(1)=PROMEDIO(B2:B1001) (2)=DESVEST(B2:B1001) (3)=MIN(B2:B1001) (4)=MAX(B2:B1001) (5)=INTERVALO.CONFIANZA(0,05;G3;CONTAR(B2:B1001)) (6)=G2-G6 (7)=G6+G2 (8)=$G$2+(-3*$G$3) (9)=$G$2+(-2*$G$3) (10)=$G$2+(-1*$G$3) (11)=$G$2+(0*$G$3) (12)=$G$2+(1*$G$3) (13)=$G$2+(2*$G$3) (14)=$G$2+(3*$G$3) (15)=FRECUENCIA(B2:B1001;H2:H8) |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabla 8. Análisis estadístico de la simulación de Monte Carlo |
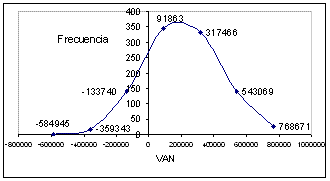
Por último con un gráfico del tipo XY (Dispersión), con puntos de datos conectados por líneas suavizadas, se representa la serie Frecuencia.
|
|
| Figura 9. Representación gráfica de la distribución de frecuencia |
4.- Conclusión
Cuando se parte de un modelo simple, se cuentan con las herramientas necesarias y se posee el suficiente conocimiento como para poder utilizarlas; el administrador tiene en sus manos todos los elementos que se requieren para poder crear buenos Sistemas de Soporte de Decisiones. En este artículo también se deja demostrando, que no se precisan ni grandes recursos, ni grandes equipos de trabajo para llevar adelante un Proyecto Informático.
6.- Agradecimientos
Ing. Ricardo Luis Marini. Investigador del Centro de Investigaciones Aplicadas (CIA), Córdoba Argentina
7.- Download archivos Microsoft Excel 97
- Para distribuciones discretas - 1_montecarlo_discreta.xls
- Para distribuciones continuas - 2_montecarlo_continua.xls
Bibliografía - Bibliography
FAULÍN, Javier, et al. Simulación de Monte Carlo con Excel. Proyecto e-Math. 🔍
NARVÁEZ, Jorge Luis. El lado Oscuro de la Estrategia, Buenos Aires: CandC, 1996 🔍
RAUIL, Coss Bu. Simulación Un enfoque práctico. México : Editorial Limusa, 1995 🔍
SEILA, Andrew F. y BANKS, Jerry. Spreadsheer Risk Analysis Using Simulation. 1990. 🔍
Google Scholar Index
Article
Publisher: