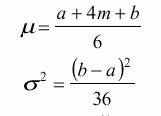PERT: una metodología simplificada

Introducción

El propósito o fin de todo proyecto debe ser especificado e indicado, mediante un objetivo que indique claramente la meta a ser alcanzada; además deberán especificarse todas y cada una de las actividades necesarias para cumplimentar tal misión, como así también las relaciones causales de dichas actividades y de dinámica que permitan establecer los tiempos requeridos. Ejecutando las operaciones necesarias para satisfacer estas especificaciones se obtendrá el objetivo final, que constituye el acontecimiento final del diagrama Program Evaluation and Review Technique (PERT).

Descripción

El Program Evaluation and Review Technique (PERT) es una técnica para el planeamiento y control de las actividades que se deberán desarrollar al momento de elaborar un proyecto; el PERT está orientado hacia la evaluación del progreso del proyecto hacia sus objetivos, concentra la atención sobre los problemas reales o potenciales del proyecto, proporciona a los responsables informes precisos del estado del mismo, predice la verosimilitud de alcanzar los objetivos y determina el espacio de tiempo en el que puede realizarse el proyecto.

Aplicaciones

El PERT es especialmente útil en aquellos programas en los que deben considerarse las relaciones causales de las actividades y su dinámica a través del tiempo; además, permite un análisis particular y general de aquellas actividades de las que si dispone poca experiencia.

Ventajas

Las principales ventajas son:

• permite una representación sistémica, por lo tanto, clara y precisa de las actividades constitutivas del proyectos, lo que a su vez facilita el proceso de comunicación,
• su técnica para la estimación del tiempo de duración de cada actividad y del proyecto en su conjunto, está sustentada en la distribución estocástica Beta,
• permite la detección de aquellas actividades críticas del proyecto que son susceptibles de demorar, o bien adelantar con el cuidado de los costos que implique, la fecha de finalización del proyecto.
• asiste al análisis de viabilidad técnica, operativa, y económica del proyecto,
• permite realizar procesos de simulación que validen la lógica del sistema propuesto, y
• facilita la tarea de control a fin de determinar el estado del proyecto en un momento determinado.

Pasos para diagramar un proyecto

Listar las actividades

Formular la lista de actividades a desarrollar; por ejemplo, de la siguiente manera:

A Estudio de factibilidad.

B Diseño general del sistema.

C Selección del personal.

D Capacitación del personal.

E Estudio de aplicaciones.

F Estudio de financiación.

G Estudio de equipos.

H Selección de equipos.

I Evaluación final.

J Programación.

K Envío de equipo.

L Recepción de equipo.

M Preparación del lugar.

N Instalación del sistema de comunicaciones.

O Instalación del equipo.

P Puesta a punto de programas.

Q Capacitación de usuarios.

R Prueba del sistema.

S Puesta a punto del sistema.

T. Operación paralela.

Indicar la secuencia lógica de las actividades

Sobre la base de la lista anterior, a título de ejemplo, se establece la secuencia lógica de las actividades.

Cuadro de secuencia lógica de operaciones

Método de cálculo

Estimaciones temporales

Suponiendo que el tiempo esperado (te) de duración de una actividad es una variable aleatoria sobre un intervalo finito; la distribución Beta, se presenta como un buen modelo para la distribución de tal variable aleatoria. Esto es así porque, una de las características en la planificación de nuevos proyectos, es la escasa información muestral disponible para ajustar la distribución, por ello se precisa recurrir al conocimiento subjetivo de los expertos sobre la actividad en estudio; consecuentemente se determinan por opinión del experto tres duraciones: una optimista, otra pesimista y otra más probable.

Entonces, una vez que se ha logrado un cuadro, con los detalles adecuados de tiempos y precedencias, es necesario establecer la estimación de la duración de cada una de las actividades, a saber:

• Duración Optimista (to): tiempo que se necesita para efectuar la actividad si no se presentan dificultades o complicaciones imprevistas. En la mayoría de los casos la probabilidad de realizar la actividad en este tiempo es pequeña; una regla práctica para este caso es que la probabilidad de realizar la actividad en un tiempo menor que la duración optimista es del uno por ciento .
• Duración más probable (tm): tiempo más probable que necesite la actividad para su realización. Esta estimación debe tener en cuenta las circunstancias normales, considerando algunos retrasos debidos a circunstancia poco habituales, y debe estar basada en la mejor información, basada en evidencias relevantes, con la que pueda disponerse.
• Duración Pesimista (tp): tiempo que se necesita para efectuar la actividad si se presentaran dificultades y complicaciones inesperadas. La regla práctica en este caso es que: sólo exista una probabilidad de un uno por ciento de realizar la actividad en un tiempo mayor que la estimación pesimista.

Los creadores del PERT sugirieron estimar los valores de la media y de la varianza de la distribución beta mediante las siguientes formulas:

en nuestro caso a=to, m=te, y b=tp

Colecta de las estimaciones de las duraciones

Las estimaciones de las duraciones las obtendrá el analista PERT de las personas profesionalmente capacitadas o experimentadas, que tienen la responsabilidad de efectuar el trabajo que representan las actividades. Las estimaciones se obtendrán siguiendo rigurosamente el modelo estocástico asumido.

El diagrama PERT

El gráfico

El gráfico PERT, es la representación gráfica de las relaciones entre todos los acontecimientos y actividades necesarias para realizar un proyecto, en donde:

• un acontecimiento (representado por una elipse) es un instante específico del tiempo. Un acontecimiento puede ser el principio o el fin de una actividad, un punto en el tiempo que puede ser reconocido e identificado claramente.
• Una actividad (representada por una flecha) es el trabajo necesario para alcanzar un acontecimiento. Una actividad no puede iniciarse hasta que todas las actividades predecesoras hayan sido finalizadas.

Así un gráfico está compuesto por un cierto número de acontecimientos ligados entre sí mediante actividades.

El gráfico comienza con un único acontecimiento inicial, se ramifica en varios caminos que ligan diversos acontecimientos, y termina en un acontecimiento final que señala el fin del proyecto.

Puesto que el PERT es una técnica orientada hacia los acontecimientos, el interés se centra en la dinámica del sistema.

Reglas básicas

Regla 1: Se usa una, y sólo una flecha para representar una actividad a ejecutarse.

Regla 2: El diagrama se construye conectando, bajo una relación causal, flechas que representa actividades, considerando para cada una, las tres preguntas siguientes:

1 qué precede inmediatamente a esta actividad,

2 qué sigue inmediatamente a esta actividad, y

3 qué actividades son concurrentes.

Regla 3: Iniciar el diagrama con una flecha preliminar.

Regla 4: Enumerar los acontecimientos.

Regla 5: Utilice las actividades ficticias, solo cuando precise mantener la lógica del diagrama.

Numeración de los acontecimientos

Cuando la numeración comienza en el acontecimiento inicial y prosigue secuencialmente a través del gráfico, cada acontecimiento sucesor posee un número mayor que sus predecesores. De esta forma el circuito puede detectarse fácilmente, puesto que una actividad tendrá un número mayor en la cola del arco que en la cabeza.

Actividades virtuales y duraciones ficticias

El gráfico PERT se ha definido como una representación gráfica del proyecto, donde el gráfico en sí mismo es una imagen de los trabajos que se deben efectuar y de los acontecimientos que deben producirse. En algunas oportunidades, para conservar la lógica procedimental, pueden utilizarse la representación de actividades virtuales con duraciones ficticias; en donde, una actividad virtual no indica la realización de trabajo u operación real; su representación ayuda a conservar la lógica del gráfico.

Bibliografía

.Harry F. Evarts, Introducción al PERT, Sagitario S.A. Barcelona, 1965

Herrerías Pleguezuelo, Rafael. Programación, Selección y Control de Proyectos en Ambiente de Incertidumbre

Parro Nereo Roberto, Programación por camino crítico, Administración de Empresas T.III, P.289 A 341

Perissé, Marcelo Claudio. Simulación de Montecarlo para la distribución Beta en PERT. Planilla de cáldulo