|
|
|
 Características
de la distribución probabilística normal
Véalo
aquí
La curva normal tiene forma de campana con un solo pico justo
en el centro de la distribución.
La media, mediana y moda de la distribución aritmética son iguales
y se localizan en el pico.
La mitad del área bajo la curva está a la derecha del pico, y la
otra mitad está a la izquierda.
La distribución normal es simétrica respecto a su media.
La distribución normal es asintótica - la curva se acerca cada vez
más al eje x pero en realidad nunca llega a tocarlo.
Distribución normal estándar
Vealo
aquí
Una distribución normal que tiene media igual a 0 y desvición
estándar igual a 1 se denomina distribución normal estándar.
Valor z: la distancia entre un valor seleccionado, designado como
X, y la población media μ, dividida entre la desviación estándar
de la población σ,
Ejemplo
El ingreso mensual que una corporación grande
ofrece a los graduados en MBA tiene una distribución normal con
media de $2000 y desviación estándar de $200.
¿Cuál es el valor z para un ingreso de $2200? y
¿cuál para uno de $1700?
Para X = $2200, z = (2200 - 2000) /200 = 1.
Para X = $1700, z = (1700 - 2000) /200 = - 1.5
Un valor z igual a 1 indica que el valor de $2200
es mayor que la desviación estándar de la media de $2000,
así como el valor z igual a -1.5 indica que el
valor de $1700 es menor que la desviación estándar de la media de
$2000.
Áreas bajo la curva normal
Véalo
aquí
Cerca de 68% del área bajo la curva normal está a menos de una
desviación estándar respecto a la media.μ ± 1
σ
Alrededor de 95% está a menos de dos desviaciones estándar de la
media.μ ± 2 σ
99.74% está a menos de tres desviaciones estándar de la media.μ
± 3 σ
Ejemplo:
El consumo de agua diario por persona en New
Providence, Nueva Jersey tiene una distribución normal con media
de 20 galones y desviaición estándar de 5 galones.
Cerca de 68% del consumo de agua diario por persona en New
Providence está entre cuáles dos valores.
. Esto es, cerca de 68% del consumo diario de agua está entre 15 y
25 galones.
¿Cuál es la probabilidad de que una persona de New
Providence seleccionada al azar use menos de 20 galones por día?
El valor z asociado es z = (20 - 20) /5 = 0. Así, P(X<20) = P(z<0)
= .5
¿Qué prcentaje usan entre 20 y 24 galones?
El valor z asociado con X = 20 es z = 0 y con X = 24, z = (24 -
20) /5 = .8. Así, P(20<X<24) = P(0<z<.8) = 28.81%
¿Qué porcentaje de la población utiliza entre 18
y 26 galones?
El valor z asociado con X = 18 es z = (18 -20) /5 = -.4, y para X
= 26, z = (26 - 20) /5 = 1.2. Así, P(18<X<26) = P(-.4<z<1.2) =
.1554 + .3849 = .5403
El profesor Mann determinó que el promedio final en su curso de
estadística tiene una distribución normal con media de 72 y
desviación estándar de 5. Decidió asignar las calificaciones del
curso de manera que 15% de los alumnos reciban una calificación de
A. ¿Cuál es el promedio más bajo que un alumno puede tener para
obtener una A?
Sea X el promedio más bajo. Encuentre X de manera que P(X > X) =
.15. El valor z correspondiente es 1.04. Así se tiene (X - 72) / 5
= 1.04, o X = 77.2
La cantidad de propina que un mesero recibe por
turno en un restaurante exclusivo tiene una distribución normal
con media de $80 y desviación estándar de $10. Shelli siente que
ha dado un mal srvicio si el total de sus propinas del turno es
menor que $65. ¿Cuál es la probabilidad de que ella haya dado un
mal servicio?
Sea X la cantidad de propina. El valor z asociado con X = 65 es z
= (65 - 80) /10 = -1.5. Así P(X<65) = P(z<-1.5) =.5 - .4332 =
.0668.
Aproximación
normal a la binomial
Véalo
aquí
Utilizar la distribución normal (una distribución continua)
como sustituto de una distribución binomial (una distribución
discreta) para valores grandes de n, parece razonable porque
conforme n aumenta, una distribución binomial se acerca más a una
distribución normal.
La distribución de probabilidad normal, en general, se considera
una buena aproximación a la binomial cuando
n y n(1 - ) son ambos mayores que 5.
Recuerde el experimento binomial :
existen sólo dos resultados mutualmente excluyentes (éxito o
fracaso) en cada ensayo.
una distribución binomial es el resultado de contar el número de
éxitos en una cantidad fija de ensayos.
cada ensayo es independiente.
la probabilidad es fija de un ensayo a otro, y el número de
ensayos n también es fijo.
Distribución binomial para n igual a 3 y 20, donde
p =.50.
Factor de corrección por continuidad
El valor .5 se resta o se suma, dependiendo del problema, a un
valor seleccionado cuando una distribución de probabilidad
binomial (una distribución discreta) se aproxima por una
distribución de probabilidad continua (la distribución normal).
Un estudio reciente de una compañía de investigación de
mercados mostró que 15% de las casas en Estados Unidos poseen una
cámara de video. Se obtuvo una muestra de 200 casas.
De las 200 casas en la muestra ¿cuántas se espera que tengan una
cámara de video?
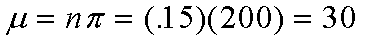¿Cuál es la variancia?
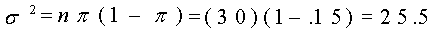
¿Cuál es la desviación estándar?
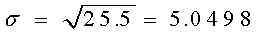
¿Cuál es la probabilidad de que menos de 40 casas de la muestra
tengan cámara de video?
Se necesita P(X<40) = P(X< 39).
Así, Al usar la aproximación normal,
P(X<39.5) P[z (39.5-30)/5.0498] =
P(z 1.8812) P(z<1.88)=.5+.4699 +.9699
.
|
|
